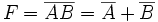Portes Logiques : Fonctionnement, Types et Équations Booléennes
Classé dans Informatique
Écrit le en  français avec une taille de 4,66 KB
français avec une taille de 4,66 KB
Introduction aux Portes Logiques
Une porte logique est un dispositif électronique qui est l'expression physique d'un opérateur booléen logique, agissant comme un interrupteur. Chaque porte logique est constituée d'un réseau de dispositifs de commutation qui remplit les conditions spécifiques à l'opérateur booléen qu'elle représente. Elles sont essentiellement des circuits de commutation intégrés dans une puce.
Claude Elwood Shannon a expérimenté avec des relais ou des commutateurs électromagnétiques pour réaliser les conditions de chaque porte logique. Par exemple, pour la fonction booléenne ET (AND), il a placé des interrupteurs en série : si un seul d'entre eux est « ouvert », la sortie de la porte est 0. Pour la mise en œuvre d'une porte OU (OR), il a relié les commutateurs en parallèle.
Types de Portes Logiques Fondamentales
- Porte NOR (NON-OU)
- Porte XNOR (OU Exclusif Négatif)
- Porte ET (AND)
- Porte OU (OR)
- Porte OU Exclusif (XOR)
- Porte NON (NOT)
- Porte NAND (NON-ET)
Porte Logique NOR (NON-OU)
La porte logique NOR, mieux connue sous son nom anglais NOR, effectue la somme logique inversée. Le symbole de cette porte peut être vu ci-contre dans les schémas électroniques.
L'équation décrivant le comportement caractéristique de la porte NOR est :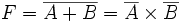
Porte Logique XNOR (OU Exclusif Négatif)
La porte logique d'équivalence, connue sous son nom anglais XNOR, exécute la fonction booléenne AB + A'B'. Le symbole de cette porte peut être vu ci-contre dans les schémas électroniques.
L'équation décrivant le comportement caractéristique de la porte XNOR est :
Porte Logique ET (AND)
La porte logique ET (AND), connue sous son nom anglais AND, exécute la fonction booléenne de produit logique. Son symbole est un point (·), bien qu'il soit habituellement omis. Ainsi, les variables logiques A et B sont indiquées comme AB, et se lisent « A et B » ou simplement « A B ».
L'équation décrivant le comportement caractéristique de la porte ET est :
Porte Logique OU (OR)
La porte logique OU (OR), mieux connue sous son nom anglais OR, effectue la somme logique.
L'équation décrivant le comportement caractéristique de la porte OR est :
Porte Logique OU Exclusif (XOR)
La porte logique OU Exclusif (XOR), mieux connue sous son nom anglais XOR, effectue la fonction booléenne A'B + AB'. Son symbole est le signe plus (+) inscrit dans un cercle. Le symbole de cette porte peut être vu ci-contre dans les schémas électroniques.
L'équation décrivant le comportement caractéristique de la porte XOR est : |
| 
Porte Logique NON (NOT)
La porte logique NON (NOT en anglais) exécute la fonction booléenne d'inversion ou de négation d'une variable logique. Une variable logique A à laquelle la négation est appliquée se prononce « non A » ou « A barré ».
L'équation décrivant le comportement caractéristique de la porte NON est :
Porte Logique NAND (NON-ET)
La porte logique NON-ET (NAND), connue sous son nom anglais NAND, effectue le produit logique inversé. Le symbole de cette porte peut être vu ci-contre dans les schémas électroniques.
L'équation décrivant le comportement caractéristique de la porte NAND est :