Statistiques Descriptives : Exercices et Solutions

Exercice 1 : Nombre de Personnes par Foyer

Lorsque nous avons demandé à 20 personnes le nombre de personnes vivant dans leur foyer, nous avons obtenu les réponses suivantes :

Questions

a) Faire un tableau de fréquences absolues et fréquences relatives.

b) Tracer le graphique de la distribution (en utilisant les fréquences absolues).

Solution

a)

b)

Exercice 2 : Nombre de Téléphones par Foyer

Une compagnie de téléphone souhaite connaître le nombre de téléphones (y compris les téléphones mobiles) présents dans les logements. Une enquête a été réalisée et les réponses suivantes ont été obtenues :

Questions

a) Faire un tableau de fréquences absolues et fréquences relatives.

b) Tracer le graphique de la distribution (en utilisant les fréquences absolues).

Solution

a)

b)

Exercice 3 : Résultats d'un Test à Choix Multiples

Dans une classe, un test à choix multiples de 40 questions a été réalisé. Le nombre de réponses correctes obtenues par chacun des élèves est le suivant :

Questions

a) Résumer les données en utilisant un tableau de fréquences absolues et fréquences relatives.

b) Tracer le graphique de cette distribution (en utilisant les fréquences absolues).

Solution

a)

b)

Exercice 4 : Jours de Sport par Semaine

Nous avons demandé à 20 personnes le nombre moyen de jours par semaine où elles font du sport. Voici les réponses obtenues :

Questions

a) Faire un tableau de fréquences absolues et fréquences relatives.

b) Tracer le graphique de la distribution (en utilisant les fréquences absolues).

Solution

a)

b)

Exercice 5 : Résultats de Lancers de Dé

Nous avons lancé un dé 20 fois et avons consigné les résultats :

Questions

a) Trier les données dans un tableau de fréquences absolues et fréquences relatives.

b) Tracer le graphique de la distribution (en utilisant les fréquences absolues).

Solution

a)

b)

Exercice 6 : Temps de Sprint

Lors d'un sprint, le temps mis par chaque participant pour parcourir une distance fixe a été chronométré. Les temps, en secondes, sont les suivants :

Questions

a) Faire un tableau de fréquences, en regroupant les données en intervalles de longueur 1, à partir de 8.

b) Tracer le graphique de la distribution.

Solution

a)

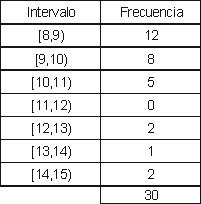
b)

Exercice 7 : Heures d'Étude par Semaine

Dans une classe, on a demandé aux élèves le nombre d'heures qu'ils consacrent à l'étude par semaine. Les réponses sont les suivantes :

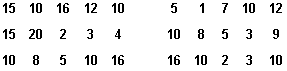
Questions

a) Trier les données dans un tableau de fréquences, en les regroupant en intervalles de longueur 3, en commençant à 0.

b) Tracer le graphique de la distribution.

Solution

a)

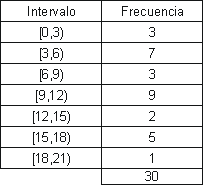
b)

Exercice 8 : Taille de 30 Personnes

Nous avons mesuré la taille, en centimètres, de 30 personnes. Voici les résultats :

Questions

a) Faire un tableau de fréquences, en regroupant les données en intervalles de longueur 5, en commençant à 146,5.

b) Tracer le graphique de la distribution.

Solution

a)

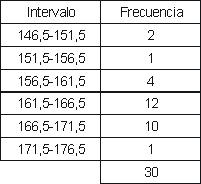
b)

Exercice 9 : Âge de 30 Personnes

Dans un groupe de 30 personnes, l'âge de chacun a été relevé. Voici les résultats :

Questions

a) Faire un tableau de fréquences, en regroupant les données en intervalles de longueur 5, en commençant à 0.

b) Tracer le graphique de la distribution.

Solution

a)

b)

Exercice 10 : Poids de 30 Enfants

Un examen médical a été mené dans un groupe de 30 enfants. L'une des données relevées est le poids en kilogrammes de chacun. Voici les résultats :

Questions

a) Faire un tableau de fréquences, en regroupant les données en intervalles de longueur 3, en commençant à 24,5.

b) Tracer le graphique de la distribution.

Solution

a)

b)

Exercice 11 : Notes d'un Test de Mathématiques

Les notes obtenues dans une classe lors d'un test de mathématiques sont énumérées dans le tableau suivant :

Questions

a) Trouver la moyenne et l'écart type.

Solution

a)

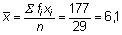
Le score moyen est de 6,1, avec un écart type de 2,27.

Exercice 12 : Temps de Trajet en Bus Scolaire

Dans un bus scolaire, on a demandé aux élèves le temps qu'il leur faut pour aller de leur domicile à l'arrêt de bus. Les résultats sont présentés dans le tableau suivant :

Questions

Calculer la moyenne et l'écart type de cette distribution.

Solution

Nous avons trouvé la marque de classe, x_i, pour chaque intervalle de mesure et le tableau :

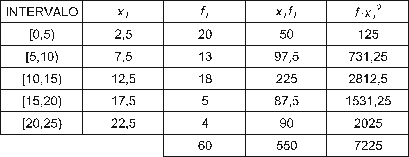
Les élèves mettent, en moyenne, 9,17 minutes, avec un écart type de 6,03 minutes.

Exercice 13 : Composition des Ménages

Lorsqu'on a demandé à 50 familles le nombre de personnes qui composent leur foyer, nous avons obtenu les informations contenues dans le tableau suivant :

Questions

a) Trouver la moyenne et l'écart type.

Solution

a)

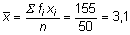
Le nombre moyen de personnes qui composent le ménage est de 3,1, avec un écart type de 1,1 personnes.

Exercice 14 : Distribution d'Âge

Trouver la moyenne et l'écart type pour la distribution d'âge suivante :

Solution

Nous avons trouvé la marque de classe, x_i, pour chaque intervalle de mesure et le tableau :

L'âge moyen est de 15,5 ans avec un écart type de 6,71 années.

Exercice 15 : Lancers de Dé (100 fois)

Nous avons lancé un dé 100 fois, en enregistrant le résultat à chaque fois. L'information est reflétée dans le tableau suivant :

Questions

a) Trouver la moyenne et l'écart type.

Solution

a)

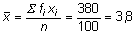
Nous avons obtenu une note moyenne de 3,8, avec un écart type de 1,75 points.

Exercice 16 : Comparaison de la Dispersion de Notes

La moyenne d'une classe A, sur un test a été de 5,5, avec un écart type de 2,1. Dans une autre classe, B, la note moyenne dans le même test a été de 7,3 et l'écart type de 2,6. Calculer le coefficient de variation et comparer la dispersion des deux groupes.

Solution

Exercice 17 : Comparaison de la Variation des Salaires

Le salaire moyen des travailleurs d'une entreprise, A, est de 900 euros par mois, avec un écart type de 100 euros. Dans une autre entreprise, B, le salaire moyen est de 980 euros par mois avec un écart type de 150 euros. Calculer le coefficient de variation et dire laquelle des deux entreprises a une plus grande variation relative des salaires.

Solution

Exercice 18 : Comparaison de la Variation du Poids

Le poids moyen d'une espèce animale, A, est de 21,3 kg et l'écart-type est de 2,5 kg. Chez une autre espèce d'animaux, B, le poids moyen est de 125 kg et l'écart type est de 13 kg. Calculer le coefficient de variation et dire laquelle des deux espèces a une plus grande variation relative du poids.

Solution

Exercice 19 : Livres Achetés en Librairie

Dans une librairie, on a noté le nombre de livres achetés par chaque personne qui est entrée dans le magasin. Le tableau suivant résume l'information :

Questions

Calculer M, Q₁, Q₃ et p₈₀.

Solution

Nous construisons le tableau des fréquences cumulées :

50% des personnes ont acheté 2 livres ou moins, et les 50% restants ont acheté 2 livres ou plus. De même, on interprète :

Exercice 20 : Nombre de Lancers pour Obtenir Face

Nous avons lancé une pièce de monnaie et noté le nombre de lancers nécessaires pour obtenir le premier côté face. Nous avons effectué l'expérience 100 fois, avec les résultats suivants :

Questions

Calculer M, Q₁, Q₃ et p₃₀.

Solution

Nous construisons le tableau des fréquences cumulées :

50% du temps, nous avons eu besoin de 2 lancers ou moins, et les 50% restants ont eu besoin de 2 lancers ou plus. De même, on interprète :

Exercice 21 : Résultats de Lancers de Dé (120 fois)

Dans le tableau suivant, nous avons résumé les résultats obtenus en lançant un dé 120 fois :

Questions

Calculer M, Q₁, Q₃ et p₂₀.

Solution

Nous construisons le tableau des fréquences cumulées :

50% du temps, on a obtenu une note inférieure ou égale à 3, et 50% du temps, on a obtenu une note supérieure ou égale à 3. De même, on interprète :

Exercice 22 : Notes d'un Événement Sportif

Un groupe d'athlètes a obtenu les notes suivantes sur un événement sportif qui est évalué de 0 à 5 points :

Questions

Calculer M, Q₁ et Q₃.

Solution

Nous construisons le tableau des fréquences cumulées :

50% des athlètes ont obtenu une note égale ou inférieure à 4, et 50% ont obtenu une note égale ou supérieure à 4. De même, on interprète :

Exercice 23 : Calcul de Médiane, Quartiles et Percentile

Dans la distribution suivante, calculer M, Q₁, Q₃ et p₉₀.

Solution

Nous construisons le tableau des fréquences cumulées :